
Entende-se por progressão aritmética (P.A.) a sequência de números em que a diferença entre um termo e seu anterior será sempre a mesma. E tal diferença se conhece como razão da P.A.
Desse modo, a partir do segundo elemento que surge numa sequência, os que vem em seguida se tratam do resultado da soma da diferença constante com o valor do elemento que vem antes, por exemplo:
– 4, 12, 20, 28 (nesse exemplo, a constante é o número 8);
– Já se existe a sequência (4, 8, 12, 16, 20, 24, 28) a constante aqui é o número 4, que se soma em cada termo que veio após o primeiro termo.
A progressão aritmética é diferente da progressão geométrica, sendo essa última é caracteriza pelos números serem multiplicados pela razão, enquanto que na progressão aritmética os números são somados.
Para se escrever uma P.A. é usada a chamada fórmula do termo geral, que é descrita da seguinte maneira: an=a1 + r·(n-1).
P.A. finita ou P.A. infinita
As progressões aritméticas podem ainda ser classificada em P.A. finita ou P.A. infinita, dizendo respeito a quantidade de termos que as mesmas possuem.
No caso de uma P.A. finita, ela é caracterizada por dispor de uma quantidade determinada de termos. Por sua vez, a P.A. infinita possui um número infinito de termos, sendo se usam as reticências para indicar quando se terá essa quantidade infinita de termos. Veja a seguir alguns exemplos para entender melhor sobre ambas:
– Se existe a sequência (2, 6, 10, 14, 18, 22…) ela se trata de uma P.A. infinita;
– Mas se existe a sequência (28, 24, 20, 16, 12) ela se trata de uma P.A. finita.
Uma das propriedades da P.A. é que numa P.A. finita, quando se somam dois termos equidistantes dos extremos se tem o resultado que é igual ao que se teria se somassem também os extremos, por exemplo:
– Na sequência (3, 6, 9, 12, 15, 18, 21), a soma dos extremos dá 24 e se forem somados termos equidistantes dos extremos como 9 e 15 se teria também o mesmo resultado.
Mais propriedades da P.A.
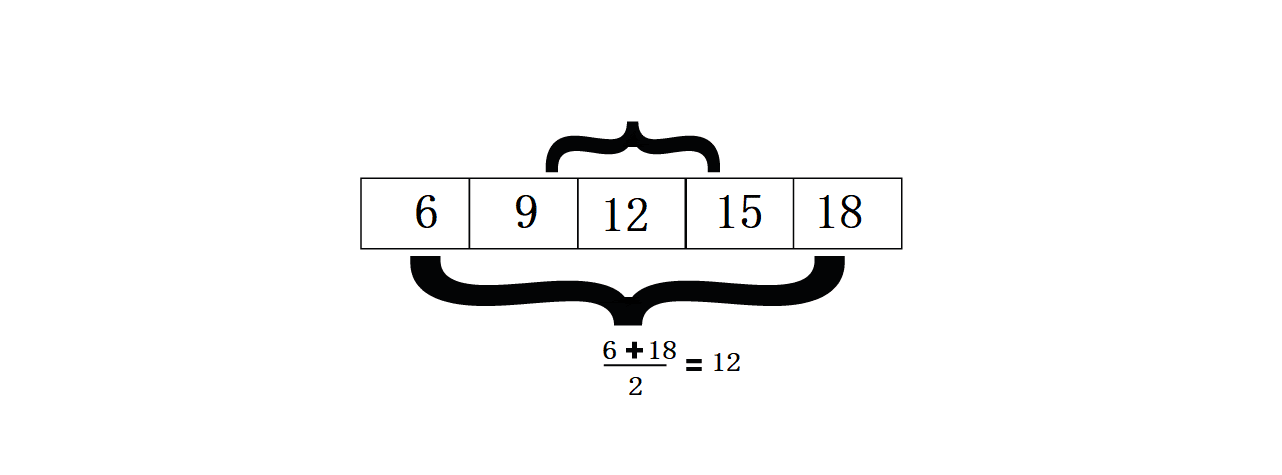
Outra propriedade importante do P.A. é que se for levada em consideração uma sequência com três termos (consecutivos), então o termo que está no meio será sempre igual a média aritmética dos outros termos (que estão um de cada lado), por exemplo:
– Numa sequência de P.A. (12, 15, 18), se os termos 12 e 18 e forem somados e o resultado for dividido por 2 se teria o número 15, que é o número do meio dessa sequência de três números.
Mais uma propriedade diz respeito a uma P.A. finita. Se há uma progressão aritmética finita que traz números que são ímpares, então o termo que se encontra no meio será semelhante à média aritmética existente entre os termos que são equidistantes nessa sequência. Por exemplo:
– Tendo a sequência (6, 9, 12, 15, 18, 21, 24, 27, 30), os extremos são os números 6 e 30, que quando somados dão 36, que quando e dividido gera o número 18, que é o termo central dessa progressão aritmética.
Representação dos termos
Os termos de uma progressão aritmética são identificados de acordo com a posição que ocupam numa sequência, sendo que a representação de cada um deles é feita com ouso de uma letra (que em muitas vezes acaba sendo a letra “a”) acompanhada de um número que faz a identificação da posição daquele termo na sequência. Veja a seguir um exemplo:
– Se temos a seguinte P.A. (4, 8, 12, 16, 20) e for usada a representação dos termos a3, isso quer dizer que se trata do número 12 nessa sequência;
– E se temos a mesma P.A. (4, 8, 12, 16, 20) e for usada a representação dos termos a4, isso quer dizer que se trata do número 16 nessa sequência;
– Já se temos a P.A. (1, 3, 5, 7, 9, 11, 13) e for usada a representação dos termos a3, isso quer dizer que se trata do número 5 nessa sequência;
– E com a mesma P.A. (1, 3, 5, 7, 9, 11, 13), for usada a representação dos termos a5, isso quer dizer que se trata do número 9 nessa sequência.
Classificação da P.A.
As P.A. se classificam segundo o valor da razão, desse modo se teriam as seguintes classificações:
– Constante: uma P.A. é classificada como constante se a razão for igual a zero. No exemplo com a sequência: (5, 5, 5, 5, 5, 5) se tem a constante com a razão 0 (r = 0), uma vez que entre 5 e 5 não existe um termo;
– Crescente: já numa constante crescente a razão é maior do que zero. No exemplo com a sequência: (3, 6, 9, 12, 15, 18, 21) se tem a constante com a razão 3 (r = 3), isso que dizer que a diferença entre um termo e o que está antes dele é sempre um número 3;
– Decrescente: já numa P.A. decrescente se tem uma razão que é menor do que zero. Veja a sequência a seguir: (12, 9, 6, 3, 0, – 3, – 5, …), nesse caso, a razão é – 3. Desse modo, nessa progressão aritmética a sua razão será sempre negativa, com cada termo que vem a seguir sendo menor do que o termo anterior, sendo que com isso os valores dos termos vão se reduzindo, ou seja decrescer.
SOUSA, Priscila. (23 de Dezembro de 2022). Progressão aritmética - O que é, conceito, propriedades e classificação. Conceito.de. https://conceito.de/progressao-aritmetica
