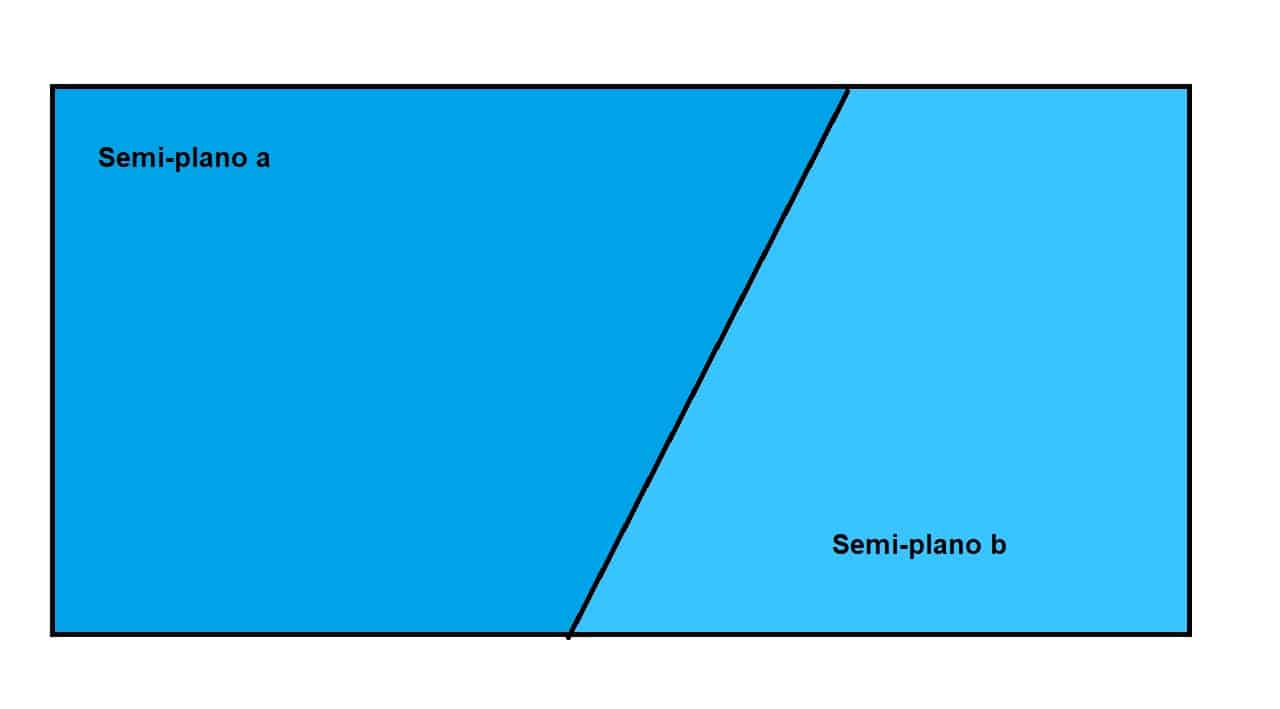
O conceito de semi-plano é utilizado no âmbito da geometria para denominar as porções de um plano que estão delimitadas por qualquer das suas rectas. Cabe destacar que cada recta divide o plano em duas porções (isto é, em dois semi-planos).
Para entender o que é um semiplano, é imprescindível compreender a noção de plano. Pode-se dizer que um plano é um objecto geométrico ideal que alberga uma quantidade infinita de rectas e de pontos e que tem apenas duas dimensões. O plano, a recta e o ponto são os conceitos essenciais da especialidade da matemática que conhecemos pelo nome de geometria.
Os planos, por conseguinte, dividem-se em semi-planos pelas rectas que o atravessam. Cada uma das rectas, deste modo, dá origem a dois semiplanos no plano. Estes semi-planos, obviamente, não têm necessariamente as mesmas dimensões.
As leis da geometria indicam que por cada dois semi-planos criados por uma recta x existe uma quantidade infinita de pontos. Todo ponto pertencente ao plano em questão, por outro lado, pertence a algum dos dois semi-planos determinados pela recta ou à própria recta.
Dois pontos contidos no mesmo semi-plano, além do mais, formam um segmento que não se cruza com a recta x, ao passo que dos pontos contidos em diferentes semi-planos criam um segmento que corta a recta x.
Tipos de semi-planos
Da mesma forma, não nos podemos esquecer que existem dois tipos fundamentais de semi-planos:
-Semi-plano aberto, sendo aquele no qual a intersecção é a recta borde comum. Ou seja, que não contem a linha que o cruza.
-Semi-plano fechado. Sob esta denominação encontra-se o semiplano que, ao contrário do anterior, contem a dita linha encarregue de o delimitar.
Posto isto:
Se o semiplano 1 albergar o ponto P e o semiplano 2 contiver o ponto S, logo o segmento PS cortará a recta X. Por outro lado, se o semiplano 1 contar com os pontos P e W, o segmento PW não cortará a recta.
Assim sendo, há outros dados de interesse que vale a pena conhecer deste elemento que aqui nos importa, como acontece com os seguintes:
-Qualquer ponto de um plano pertence à recta da divisão ou então a um dos tais semi-planos.
-Qualquer segmento que esteja determinado por dois dos pontos do mesmo semi-plano não corta com a chamada recta de divisão. Antes pelo contrário, qualquer segmento que esteja determinado por dois pontos dos diferentes semi-planos, nesse caso sim, corta a tal recta de divisão.
Além do mais, não podemos ignorar o facto de haver diferentes tipos de semi-planos que se converteram em elementos fundamentais da Geometria, como é o caso, por exemplo, do chamado semi-plano de Poincaré ou semiplano superior de Poincaré, que foi descoberto pelo matemático que lhe deu o nome.
Basicamente sob esta denominação encontra-se um modelo de semi-plano que é eixo fundamental da geometria hiperbólica e que se conhece enquanto semi-plano superior. Tem a particularidade de tomar a parte superior do plano cartesiano embora sem “colher” o eixo x.
Semirreta, semiplano/semi-plano e semiespaço

É importante abordar ainda que o conceito de reta, plano e também espaço estão ligados estritamente aos conceitos de semirreta, semiplano e semiespaço. Para um melhor entendimento, há a seguir uma explicação sobre cada um deles.
Recta (ou reta, no português no Brasil) ou semi-recta (semirreta no Brasil)
A recta ou reta se trata de um conjunto de pontos infinito, sem limites, qual não realiza curva. Já a semi-recta ou semirreta caracteriza-se na porção de uma reta que se inicia em um ponto qualquer e vai até uma das suas direções. Desse modo, um ponto é capaz de fazer a divisão de uma reta de modo que resulte em duas semirretas.
Plano e semiplano/semi-plano
Os planos se tratam de superfícies ilimitadas e que não fazem curva. Enquanto isso, se obtém semiplanos quando um plano é dividido em dois por uma reta. Desse modo, com essa divisão, o plano então terá começo, porém não terá um fim. Caso haja dois pontos em um mesmo semiplano, então os pontos do segmento de reta desses se encontrarão também nesse semiplano.
Através dos semi-planos se consegue a definição dos polígonos convexos. E para fazer isso é necessário que o polígono se encontre no mesmo semiplano constituído pelos seus lados.
Nos semi-planos, uma recta que fez a divisão dos planos, e estando os pontos em semi-planos diferentes, pode concorrer com a reta que possui esses pontos.
Espaço (geometria)
Por fim, ao conjunto dos planos dá-se o nome de espaço. O mesmo se caracteriza por ser ilimitado e também infinito para qualquer direção, estando ali as figuras geométricas e também as formas geométricas. O espaço é composto por tudo o que rodeia os seres.
Quando ocorre a divisão do espaço por uma recta, resultando em duas partes, se tem um semiespaço. Se existe uma caixa e a mesma é dividida ao meio, haverá então duas partes, sendo que essas representariam os chamados semiespaços.
É possível fazer uso dos semiespaços para a determinação dos poliedros convexos. Caso as faces do poliedro estejam cada uma localizadas num plano que faz a determinação de dois semiespaços, sendo que o poliedro se encontra por completo num desses espaços, então se tem um poliedro que é convexo.
Todos esses conceitos são estudados na chamada geometria espacial, que é um ramo da geometria preocupado em estudar sobre as figuras no espaço (figuras que possuem mais do que duas dimensões).
Equipe editorial de Conceito.de. (31 de Julho de 2016). Atualizado em 3 de Novembro de 2022. Semi-plano - O que é, conceito, tipos e no Brasil. Conceito.de. https://conceito.de/semi-plano
